理想タンパク質構造のデザインの原理
古賀信康・古賀 (巽) 理恵
(米国Washington大学Department of Biochemistry)
email:古賀信康,古賀 (巽) 理恵
DOI: 10.7875/first.author.2012.147
Principles for designing ideal protein structures.
Nobuyasu Koga, Rie Tatsumi-Koga, Gaohua Liu, Rong Xiao, Thomas B. Acton, Gaetano T. Montelione, David Baker
Nature, 491, 222-227 (2012)
タンパク質はほどけたひもの状態からアミノ酸配列にしたがい固有の三次元の立体構造に自発的に折りたたむ.自然界のタンパク質の構造は機能の制約と中立進化の結果により局所的にエネルギーの不安定な部分を含み,折りたたみだけには最適化されておらず,このことが,アミノ酸配列はどのような原理により折りたたみののちの構造を決定しているのか,という折りたたみ問題の解明を困難にしている.この研究では,局所および非局所における相互作用が完全に整合して天然構造を安定化している“理想タンパク質構造”のデザインの原理を探ることにより,折りたたみ問題にせまった.整合する局所の構造(二次構造パターン)と非局所の構造(三次構造モチーフ)に関するいくつかのルールを発見することにより,漏斗型のエネルギー地形をもつαヘリックスおよびβストランドの両方からなるタンパク質をシステマティックにデザインする方法を確立した.この方法を用いて5つの異なるトポロジーをもつ理想タンパク質構造をデザインしたところ,デザインされたタンパク質は単量体かつ高温でも変性しない安定な構造を形成し,水溶液における構造は計算機によるシミュレーションと正確に一致していた.これらの結果は,折りたたみ問題の一端を解明するものであり,また,完全にゼロから機能性タンパク質を設計するための新しい道を切り開くものである.
タンパク質は固有の三次元の立体構造に折りたたむため,ファネル(漏斗)型のエネルギー地形をもつ.このエネルギー地形は,異なる多くの非共有結合性の相互作用が折りたたみののちの構造(天然構造)をそれ以外の非天然構造よりはるかに安定にしていることから生じる.しかしながら,ファンデルワールス力,水素結合,疎水性相互作用など非共有結合性の相互作用が,無数に存在する非天然構造のなかからどのようにして選択的に天然構造を安定にしているのかはまったく自明でない.そこで,筆者らは,ある立体構造に折りたたむタンパク質を完全にゼロからデザインすることにより,この問題に挑んだ.タンパク質の折りたたみに関する仮説をたて,この仮説にしたがい計算機により立体構造のデザインを行い,デザインされたタンパク質が正しく折りたたむどうかを実験で確かめることにより仮説の正しさを検証した.
タンパク質のもつファネル型エネルギー地形をデザインするためには,天然構造を安定にしつつ1-3)(正のデザイン),非天然構造を不安定にする4,5)(負のデザイン)ようにアミノ酸配列をデザインすればよいと考えられる.しかし,非天然構造は無数に存在するため,それらすべてを考慮して非天然構造を不安定化することは不可能である.筆者らは,局所における相互作用(二次構造を決定するようなアミノ酸配列にそって近いアミノ酸残基どうしの相互作用)と,非局所における相互作用(三次構造を安定化するようなアミノ酸配列にそって遠いアミノ酸残基どうしの相互作用)が整合して(矛盾なくつじつまがあって)天然構造を安定化するようタンパク質の構造をデザインすれば,ファネル型エネルギー地形を容易にデザインできるという仮説をたてた6).局所および非局所での相互作用が天然構造において矛盾のないようタンパク質の構造を設計すれば,それらの相互作用が矛盾する非天然構造において,エネルギーは天然構造より不安定になるはずである7).この研究では,局所および非局所での相互作用が天然構造において完全に整合した“理想タンパク質構造”をデザインするための原理を探った.まず,ある局所における構造(二次構造パターン)と,整合して形成される三次構造モチーフとの関係を調べることから研究をはじめた.アミノ酸配列において連続する2~3個の二次構造の要素がそれら自体で相互作用して三次構造モチーフを形成している場合について,Rosettaプログラムによる折りたたみシミュレーション,および,自然界のタンパク質の構造の統計解析を行うことにより,選択的にひとつの三次構造モチーフを安定に形成するような局所における構造パターンを探った.
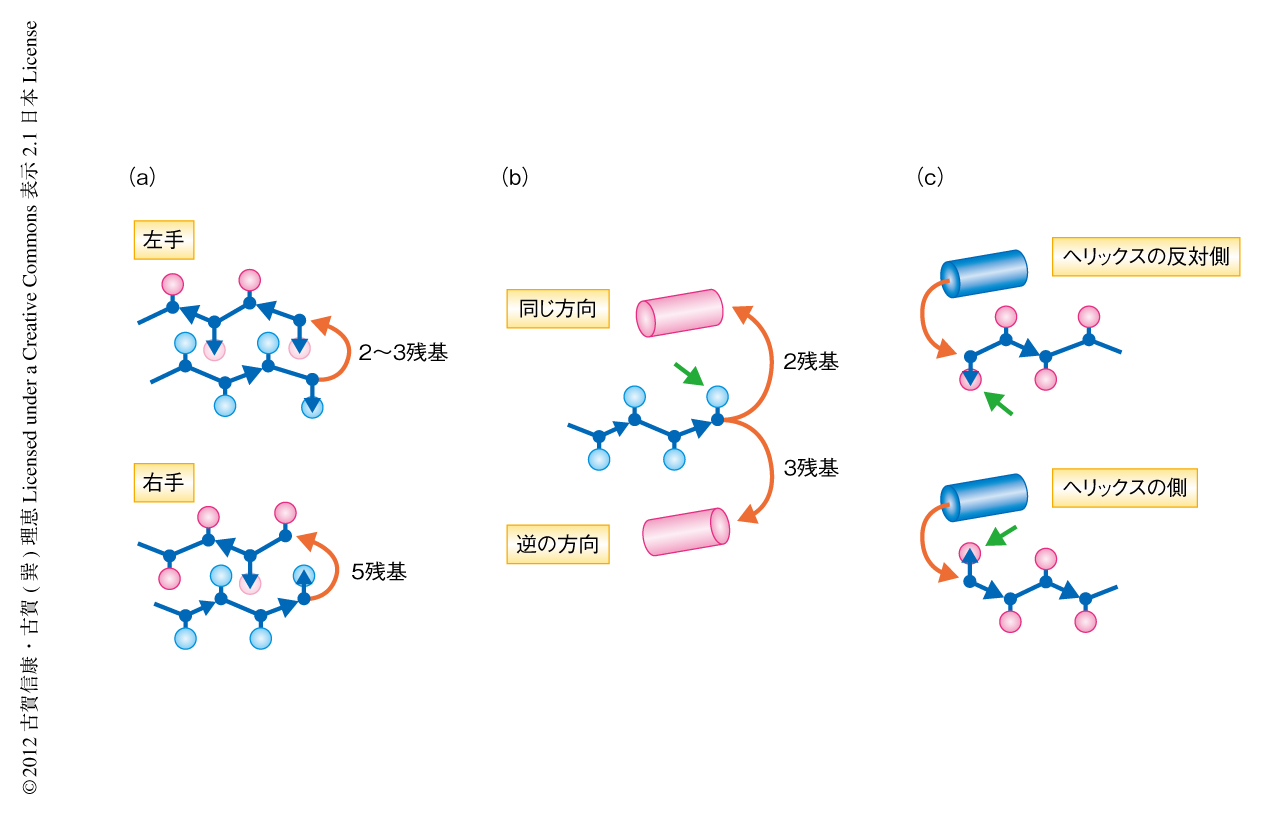
連続する2つの二次構造要素,ββ,βα,αβ(α:ヘリックス,β:ストランド)が1本のループでつながったペプチドについて,アミノ酸配列の詳細に依存しない粗視化モデルを構築し,ループの長さを変えながら伸びた構造からの折りたたみシミュレーションを行い,どのような三次構造モチーフが高い確率で形成されるのかを調べた.この粗視化モデルは,すべての主鎖原子と,1個の球で表わされた“側鎖”からなる(球のサイズはすべての残基で同じとした).エネルギー関数として,全体をコンパクトにする力,排除体積,主鎖の水素結合を考慮し,粗視化された側鎖は排除体積としてのみ扱った.折りたたみシミュレーションはモンテカルロ法により実行し,以下の3つのステップをくり返した.1)ペプチドを構成する残基からランダムに1残基を選ぶ.2)そのφψ角度に関して指定した二次構造に対応するφψ角度をランダムに選びそれに置き換える.3)エネルギー関数により全体構造を評価しメトロポリス判定法によりその構造を採用するかどうかを決定する.つまり,指定した二次構造を必ず形成するという仮定のもとで折りたたみシミュレーションを行ったとき,最終的にどのような三次構造が形成されやすいのかを観測した.このシミュレーションの結果,整合する二次構造パターンと三次構造モチーフに関するいくつかのルールが発見された(図1).さらに,これらのルールは自然界のタンパク質の構造においても観測されることが明らかになった.
[基本ルール]
ββルール:βヘアピンのキラリティはその2つのストランドのあいだにあるループの長さにより決まる(図1a).ββユニットにおけるβヘアピンのキラリティは,ループの長さが2~3残基の場合は左手の構造,5残基の場合は右手の構造を形成することを,折りたたみシミュレーションおよび自然界のタンパク質の構造解析のどちらの場合においても発見した.
βαルール:ヘリックスの位置はストランドの最後の残基のプリーツと,ストランドとヘリックスのあいだのループの長さにより決まる(図1b).βαユニットの形成する三次構造モチーフはストランドの最後の残基のプリーツ(CαCβベクトル)に対し,ヘリックスが同じ方向に位置するか,ヘリックスが逆の方向に位置するかにより分類できる.折りたたみシミュレーションおよび自然界のタンパク質の構造解析の結果,ループの長さが2残基のときにはヘリックスが同じ方向に位置する構造,3残基のときにはヘリックスが逆の方向に位置する構造を形成する傾向のあることがわかった.
αβルール:ストランドの最初の残基のプリーツはヘリックスに対し反対の方向を向く(図1c).αβユニットの形成する三次構造モチーフは,ストランドの最初の残基のプリーツがヘリックスの側を向く場合と,ヘリックスの反対側を向く場合とが考えられる.折りたたみシミュレーションおよび自然界のタンパク質の構造解析の結果,ヘリックスの側を向く構造は形成されにくいことが明らかになった.
[応用ルール]
3つの連続する二次構造要素,ββαユニット,αββユニット,βαβユニットについて折りたたみシミュレーションを行った結果,ββαユニットおよびαββユニットのキラリティ,βαβユニットの折りたたみ能力は,二次構造およびループの長さに強く依存することが明らかになり応用ルールとして定式化された.また,これら応用ルールは,さきの基本ルールの組合せの帰結として生じたものであった.
発見されたルールを用いてタンパク質の構造をデザインすれば,ファネル型エネルギー地形をもつタンパク質を容易に得られるはずである.あるトポロジーをもつタンパク質の構造をデザインするとき,ルールにしたがって二次構造とループの長さを選び三次元の主鎖構造を組み立て,その三次構造を安定にするよう正のデザインを行えば,折りたたみののちの天然構造のエネルギーを安定化すると同時に,非天然構造の負のデザインを行うことができる.なぜなら,ルールにしたがい設定した二次構造パターンが局所的に形成されれば,それとは整合しない三次構造は不安定になるからである.このアイデアを,αヘリックスとβストランドの両方からなる5つの異なるトポロジーをもつタンパク質を実際にデザインすることにより確かめた(図2).
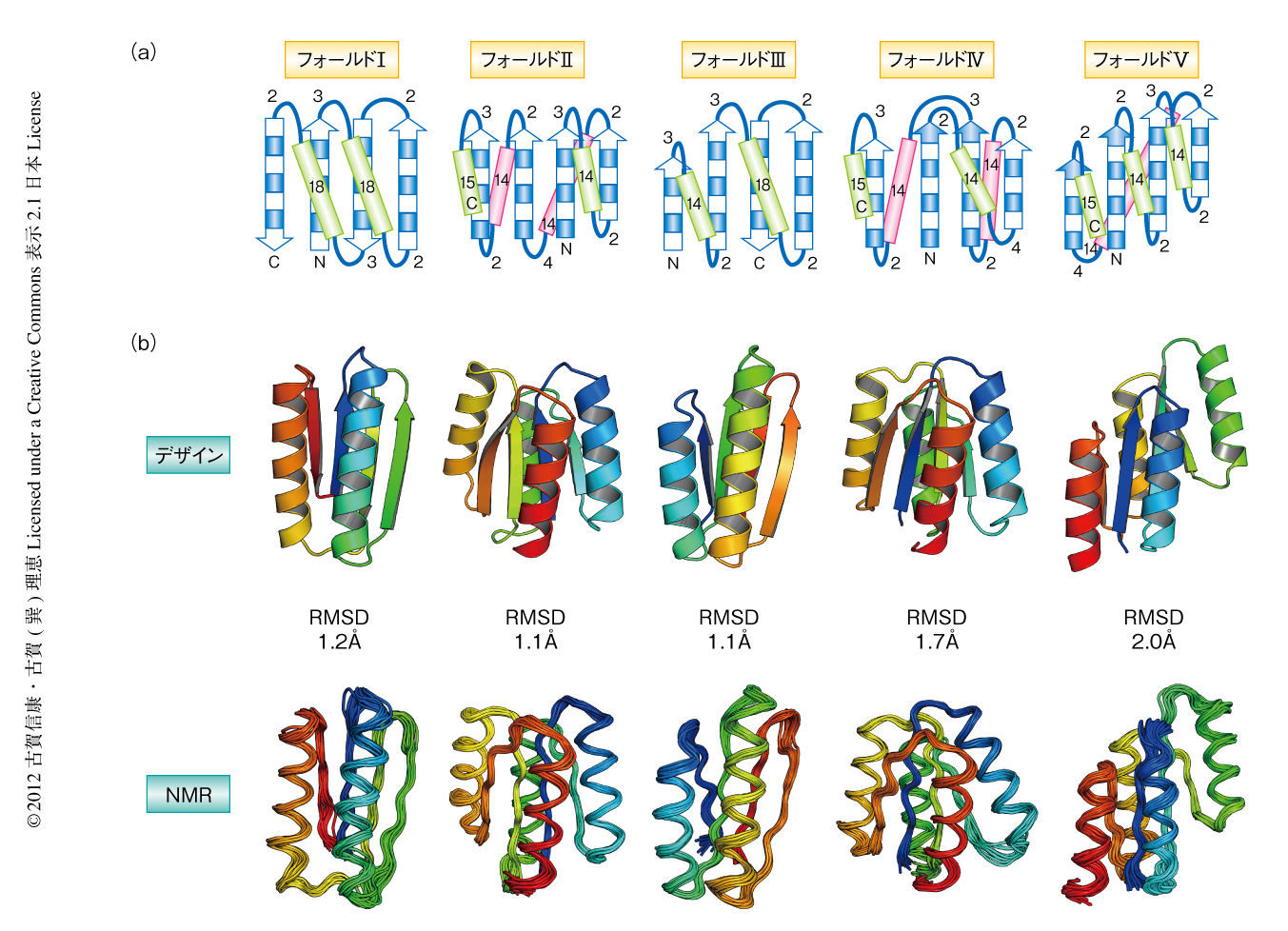
デザインの手順を示す.1)デザインするタンパク質のトポロジーについて,ルールにしたがい二次構造とループの長さを決定し,主鎖構造の設計図をかく(図2a).2)この設計図にもとづき折りたたみシミュレーションを行い,主鎖構造を構築する.このとき,できるかぎり多くの主鎖構造をつくり,βシートの湾曲,二次構造のあいだの距離や角度,ループの形状にバラエティをもたせる.このバラエティはつぎのステップにおいて密な側鎖パッキングをもつ構造をつくりだすため重要となる.3)それぞれの主鎖構造に対しこれらを安定にする側鎖構造(アミノ酸配列)を,RosettaDesign 2) を用いて設計する.このとき,疎水性相互作用が構造の安定性に重要であることを考慮し,かさ高い疎水性アミノ酸残基(イソロイシン,ロイシン,フェニルアラニン)が構造の内部に入るようにする.さらに,単量体どうしがストランドを介し多量体化するのを防ぐため,両端にあるストランドの残基(フォールドIとフォールドIIIに関しては,とくに側鎖がヘリックス側を向いている残基)に極性の残基(できれば,荷電残基)が最低ひとつは含まれるようにする.4)主鎖および側鎖の両方を微小に動かすことにより全体構造を最適化する.5)この側鎖構造のデザインと全体構造の最適化のくり返しをそれぞれの主鎖構造に対し行い,最終的に密な側鎖パッキングの実現されている構造のみを選ぶ.6)デザインされたアミノ酸配列が設定した二次構造およびループ構造を形成するかどうかを,自然界のタンパク質の統計解析データにもとづき予測し,正しく予測されたアミノ酸配列を選ぶ.6)デザインされたアミノ酸配列を使い,Rosetta@homeにおいて伸びた構造からの構造予測シミュレーション8) を行うことによりエネルギー地形を探索し,ファネル型エネルギー地形をもつアミノ酸配列に対し実験的に折りたたみ能を調べる.
このようにしてデザインされたタンパク質は,その設計において整合した局所および非局所の相互作用をもつ.特筆すべきは,これまでに新規にデザインされた唯一の球状タンパク質であるTop7 2) の主鎖構造が,ここで発見されたルールに完全にしたがっていたことである.したがって,Top7 2) も整合した局所および非局所の相互作用をもつと考えられた.
フォールドIで11個,フォールドIIで12個,フォールドIIIで14個,フォールドIVで5個,フォールドVで12個のデザインに対し,実験的に折りたたみ能を調べた.これらのアミノ酸配列は天然には相同の配列をもたない新規の配列であった.デザインされたアミノ酸配列を大腸菌に組み込んで発現および精製を行い,円偏光二色性,サイズ排除クロマトグラフィー-多角度光散乱検出,NMRにより折りたたみ能を測定した.その結果,デザインされたすべてのアミノ酸配列のうち62%が発現しかつ可溶で,αβタンパク質に特徴的な円偏光二色性スペクトルを示した.さらに,そのうち38%は単量体かつ95℃付近でも変性しない安定な構造を形成した.最終的に,1)発現,2)可溶,3)αβタンパク質に特徴的な円偏光二色性スペクトル,4)変性温度が95℃以上,5)単量体,6)シャープで分散の大きいNMRスペクトル,の6つの条件をみたしたデザインの数は,フォールドIで1個,フォールドIIで4個,フォールドIIIで3個,フォールドIVで2個,フォールドVで1個であった.これらのうち,もっともシャープで分散の大きいNMRスペクトルを示したデザインをそれぞれのトポロジーから1つ選んで,NMRにより構造を決定した.その結果,解かれた構造はデザインされた構造と正確に一致していた(図2b).また,グアニジン塩酸塩による変性実験により,デザインされたタンパク質は自然界のタンパク質にみられるよう協同的に変性し,その自由エネルギーは5 kcal/mol以上であることがわかった.
筆者らは,整合する二次構造パターンと三次構造モチーフに関するルールを発見し,このルールを用い局所および非局所の相互作用が整合して天然状態を安定にするよう立体構造を設計すれば,ファネル型エネルギー地形をもつタンパク質を容易に設計できることを示した.筆者らの発見したルールは,シミュレーションのみならず自然界のタンパク質の構造においても観測されたことから,自然界のタンパク質のファネル型エネルギー地形も同様の原理により形成されていると考えられる.つまり,自然界にあるアミノ酸配列も,ある局所の構造を安定化することにより無数にある非天然構造を不安定化しているのかもしれない7,9).
筆者らが示した理想タンパク質構造のデザインの原理は,機能性タンパク質をデザインするための新しい方法を提供するだろう.これまで,新規の機能性タンパク質をデザインする研究のほとんどは,進化によりすでにほかの機能に特化した自然界のタンパク質の構造を鋳型として行われてきた10).これからは,デザインする機能に応じタンパク質をテイラーメイドにデザインできるようになるだろう.
略歴:2006年 神戸大学大学院自然科学研究科にて博士号(理学)取得,同年 神戸大学理学部 特別研究員,2007年 京都大学大学院理学研究科 特別研究員を経て,2007年より米国Washington大学 特別研究員.
研究テーマ:タンパク質の立体構造および機能の新規デザイン.
古賀 (巽) 理恵(Rie Tatsumi-Koga)
米国Washington大学 特別研究員.
© 2012 古賀信康・古賀 (巽) 理恵 Licensed under CC 表示 2.1 日本
(米国Washington大学Department of Biochemistry)
email:古賀信康,古賀 (巽) 理恵
DOI: 10.7875/first.author.2012.147
Principles for designing ideal protein structures.
Nobuyasu Koga, Rie Tatsumi-Koga, Gaohua Liu, Rong Xiao, Thomas B. Acton, Gaetano T. Montelione, David Baker
Nature, 491, 222-227 (2012)
要 約
タンパク質はほどけたひもの状態からアミノ酸配列にしたがい固有の三次元の立体構造に自発的に折りたたむ.自然界のタンパク質の構造は機能の制約と中立進化の結果により局所的にエネルギーの不安定な部分を含み,折りたたみだけには最適化されておらず,このことが,アミノ酸配列はどのような原理により折りたたみののちの構造を決定しているのか,という折りたたみ問題の解明を困難にしている.この研究では,局所および非局所における相互作用が完全に整合して天然構造を安定化している“理想タンパク質構造”のデザインの原理を探ることにより,折りたたみ問題にせまった.整合する局所の構造(二次構造パターン)と非局所の構造(三次構造モチーフ)に関するいくつかのルールを発見することにより,漏斗型のエネルギー地形をもつαヘリックスおよびβストランドの両方からなるタンパク質をシステマティックにデザインする方法を確立した.この方法を用いて5つの異なるトポロジーをもつ理想タンパク質構造をデザインしたところ,デザインされたタンパク質は単量体かつ高温でも変性しない安定な構造を形成し,水溶液における構造は計算機によるシミュレーションと正確に一致していた.これらの結果は,折りたたみ問題の一端を解明するものであり,また,完全にゼロから機能性タンパク質を設計するための新しい道を切り開くものである.
はじめに
タンパク質は固有の三次元の立体構造に折りたたむため,ファネル(漏斗)型のエネルギー地形をもつ.このエネルギー地形は,異なる多くの非共有結合性の相互作用が折りたたみののちの構造(天然構造)をそれ以外の非天然構造よりはるかに安定にしていることから生じる.しかしながら,ファンデルワールス力,水素結合,疎水性相互作用など非共有結合性の相互作用が,無数に存在する非天然構造のなかからどのようにして選択的に天然構造を安定にしているのかはまったく自明でない.そこで,筆者らは,ある立体構造に折りたたむタンパク質を完全にゼロからデザインすることにより,この問題に挑んだ.タンパク質の折りたたみに関する仮説をたて,この仮説にしたがい計算機により立体構造のデザインを行い,デザインされたタンパク質が正しく折りたたむどうかを実験で確かめることにより仮説の正しさを検証した.
タンパク質のもつファネル型エネルギー地形をデザインするためには,天然構造を安定にしつつ1-3)(正のデザイン),非天然構造を不安定にする4,5)(負のデザイン)ようにアミノ酸配列をデザインすればよいと考えられる.しかし,非天然構造は無数に存在するため,それらすべてを考慮して非天然構造を不安定化することは不可能である.筆者らは,局所における相互作用(二次構造を決定するようなアミノ酸配列にそって近いアミノ酸残基どうしの相互作用)と,非局所における相互作用(三次構造を安定化するようなアミノ酸配列にそって遠いアミノ酸残基どうしの相互作用)が整合して(矛盾なくつじつまがあって)天然構造を安定化するようタンパク質の構造をデザインすれば,ファネル型エネルギー地形を容易にデザインできるという仮説をたてた6).局所および非局所での相互作用が天然構造において矛盾のないようタンパク質の構造を設計すれば,それらの相互作用が矛盾する非天然構造において,エネルギーは天然構造より不安定になるはずである7).この研究では,局所および非局所での相互作用が天然構造において完全に整合した“理想タンパク質構造”をデザインするための原理を探った.まず,ある局所における構造(二次構造パターン)と,整合して形成される三次構造モチーフとの関係を調べることから研究をはじめた.アミノ酸配列において連続する2~3個の二次構造の要素がそれら自体で相互作用して三次構造モチーフを形成している場合について,Rosettaプログラムによる折りたたみシミュレーション,および,自然界のタンパク質の構造の統計解析を行うことにより,選択的にひとつの三次構造モチーフを安定に形成するような局所における構造パターンを探った.
1.整合する二次構造パターンと三次構造モチーフに関するルール
連続する2つの二次構造要素,ββ,βα,αβ(α:ヘリックス,β:ストランド)が1本のループでつながったペプチドについて,アミノ酸配列の詳細に依存しない粗視化モデルを構築し,ループの長さを変えながら伸びた構造からの折りたたみシミュレーションを行い,どのような三次構造モチーフが高い確率で形成されるのかを調べた.この粗視化モデルは,すべての主鎖原子と,1個の球で表わされた“側鎖”からなる(球のサイズはすべての残基で同じとした).エネルギー関数として,全体をコンパクトにする力,排除体積,主鎖の水素結合を考慮し,粗視化された側鎖は排除体積としてのみ扱った.折りたたみシミュレーションはモンテカルロ法により実行し,以下の3つのステップをくり返した.1)ペプチドを構成する残基からランダムに1残基を選ぶ.2)そのφψ角度に関して指定した二次構造に対応するφψ角度をランダムに選びそれに置き換える.3)エネルギー関数により全体構造を評価しメトロポリス判定法によりその構造を採用するかどうかを決定する.つまり,指定した二次構造を必ず形成するという仮定のもとで折りたたみシミュレーションを行ったとき,最終的にどのような三次構造が形成されやすいのかを観測した.このシミュレーションの結果,整合する二次構造パターンと三次構造モチーフに関するいくつかのルールが発見された(図1).さらに,これらのルールは自然界のタンパク質の構造においても観測されることが明らかになった.
[基本ルール]
ββルール:βヘアピンのキラリティはその2つのストランドのあいだにあるループの長さにより決まる(図1a).ββユニットにおけるβヘアピンのキラリティは,ループの長さが2~3残基の場合は左手の構造,5残基の場合は右手の構造を形成することを,折りたたみシミュレーションおよび自然界のタンパク質の構造解析のどちらの場合においても発見した.
βαルール:ヘリックスの位置はストランドの最後の残基のプリーツと,ストランドとヘリックスのあいだのループの長さにより決まる(図1b).βαユニットの形成する三次構造モチーフはストランドの最後の残基のプリーツ(CαCβベクトル)に対し,ヘリックスが同じ方向に位置するか,ヘリックスが逆の方向に位置するかにより分類できる.折りたたみシミュレーションおよび自然界のタンパク質の構造解析の結果,ループの長さが2残基のときにはヘリックスが同じ方向に位置する構造,3残基のときにはヘリックスが逆の方向に位置する構造を形成する傾向のあることがわかった.
αβルール:ストランドの最初の残基のプリーツはヘリックスに対し反対の方向を向く(図1c).αβユニットの形成する三次構造モチーフは,ストランドの最初の残基のプリーツがヘリックスの側を向く場合と,ヘリックスの反対側を向く場合とが考えられる.折りたたみシミュレーションおよび自然界のタンパク質の構造解析の結果,ヘリックスの側を向く構造は形成されにくいことが明らかになった.
[応用ルール]
3つの連続する二次構造要素,ββαユニット,αββユニット,βαβユニットについて折りたたみシミュレーションを行った結果,ββαユニットおよびαββユニットのキラリティ,βαβユニットの折りたたみ能力は,二次構造およびループの長さに強く依存することが明らかになり応用ルールとして定式化された.また,これら応用ルールは,さきの基本ルールの組合せの帰結として生じたものであった.
2.発見されたルールを用いたファネル型エネルギー地形のデザイン
発見されたルールを用いてタンパク質の構造をデザインすれば,ファネル型エネルギー地形をもつタンパク質を容易に得られるはずである.あるトポロジーをもつタンパク質の構造をデザインするとき,ルールにしたがって二次構造とループの長さを選び三次元の主鎖構造を組み立て,その三次構造を安定にするよう正のデザインを行えば,折りたたみののちの天然構造のエネルギーを安定化すると同時に,非天然構造の負のデザインを行うことができる.なぜなら,ルールにしたがい設定した二次構造パターンが局所的に形成されれば,それとは整合しない三次構造は不安定になるからである.このアイデアを,αヘリックスとβストランドの両方からなる5つの異なるトポロジーをもつタンパク質を実際にデザインすることにより確かめた(図2).
デザインの手順を示す.1)デザインするタンパク質のトポロジーについて,ルールにしたがい二次構造とループの長さを決定し,主鎖構造の設計図をかく(図2a).2)この設計図にもとづき折りたたみシミュレーションを行い,主鎖構造を構築する.このとき,できるかぎり多くの主鎖構造をつくり,βシートの湾曲,二次構造のあいだの距離や角度,ループの形状にバラエティをもたせる.このバラエティはつぎのステップにおいて密な側鎖パッキングをもつ構造をつくりだすため重要となる.3)それぞれの主鎖構造に対しこれらを安定にする側鎖構造(アミノ酸配列)を,RosettaDesign 2) を用いて設計する.このとき,疎水性相互作用が構造の安定性に重要であることを考慮し,かさ高い疎水性アミノ酸残基(イソロイシン,ロイシン,フェニルアラニン)が構造の内部に入るようにする.さらに,単量体どうしがストランドを介し多量体化するのを防ぐため,両端にあるストランドの残基(フォールドIとフォールドIIIに関しては,とくに側鎖がヘリックス側を向いている残基)に極性の残基(できれば,荷電残基)が最低ひとつは含まれるようにする.4)主鎖および側鎖の両方を微小に動かすことにより全体構造を最適化する.5)この側鎖構造のデザインと全体構造の最適化のくり返しをそれぞれの主鎖構造に対し行い,最終的に密な側鎖パッキングの実現されている構造のみを選ぶ.6)デザインされたアミノ酸配列が設定した二次構造およびループ構造を形成するかどうかを,自然界のタンパク質の統計解析データにもとづき予測し,正しく予測されたアミノ酸配列を選ぶ.6)デザインされたアミノ酸配列を使い,Rosetta@homeにおいて伸びた構造からの構造予測シミュレーション8) を行うことによりエネルギー地形を探索し,ファネル型エネルギー地形をもつアミノ酸配列に対し実験的に折りたたみ能を調べる.
このようにしてデザインされたタンパク質は,その設計において整合した局所および非局所の相互作用をもつ.特筆すべきは,これまでに新規にデザインされた唯一の球状タンパク質であるTop7 2) の主鎖構造が,ここで発見されたルールに完全にしたがっていたことである.したがって,Top7 2) も整合した局所および非局所の相互作用をもつと考えられた.
3.デザインされたタンパク質の実験による折りたたみ能の確認
フォールドIで11個,フォールドIIで12個,フォールドIIIで14個,フォールドIVで5個,フォールドVで12個のデザインに対し,実験的に折りたたみ能を調べた.これらのアミノ酸配列は天然には相同の配列をもたない新規の配列であった.デザインされたアミノ酸配列を大腸菌に組み込んで発現および精製を行い,円偏光二色性,サイズ排除クロマトグラフィー-多角度光散乱検出,NMRにより折りたたみ能を測定した.その結果,デザインされたすべてのアミノ酸配列のうち62%が発現しかつ可溶で,αβタンパク質に特徴的な円偏光二色性スペクトルを示した.さらに,そのうち38%は単量体かつ95℃付近でも変性しない安定な構造を形成した.最終的に,1)発現,2)可溶,3)αβタンパク質に特徴的な円偏光二色性スペクトル,4)変性温度が95℃以上,5)単量体,6)シャープで分散の大きいNMRスペクトル,の6つの条件をみたしたデザインの数は,フォールドIで1個,フォールドIIで4個,フォールドIIIで3個,フォールドIVで2個,フォールドVで1個であった.これらのうち,もっともシャープで分散の大きいNMRスペクトルを示したデザインをそれぞれのトポロジーから1つ選んで,NMRにより構造を決定した.その結果,解かれた構造はデザインされた構造と正確に一致していた(図2b).また,グアニジン塩酸塩による変性実験により,デザインされたタンパク質は自然界のタンパク質にみられるよう協同的に変性し,その自由エネルギーは5 kcal/mol以上であることがわかった.
おわりに
筆者らは,整合する二次構造パターンと三次構造モチーフに関するルールを発見し,このルールを用い局所および非局所の相互作用が整合して天然状態を安定にするよう立体構造を設計すれば,ファネル型エネルギー地形をもつタンパク質を容易に設計できることを示した.筆者らの発見したルールは,シミュレーションのみならず自然界のタンパク質の構造においても観測されたことから,自然界のタンパク質のファネル型エネルギー地形も同様の原理により形成されていると考えられる.つまり,自然界にあるアミノ酸配列も,ある局所の構造を安定化することにより無数にある非天然構造を不安定化しているのかもしれない7,9).
筆者らが示した理想タンパク質構造のデザインの原理は,機能性タンパク質をデザインするための新しい方法を提供するだろう.これまで,新規の機能性タンパク質をデザインする研究のほとんどは,進化によりすでにほかの機能に特化した自然界のタンパク質の構造を鋳型として行われてきた10).これからは,デザインする機能に応じタンパク質をテイラーメイドにデザインできるようになるだろう.
文 献
- Dahiyat, B. I. & Mayo, S. L.: De novo protein design: fully automated sequence selection. Science, 278, 82-87 (1997)[PubMed]
- Kuhlman, B., Dantas, G., Ireton, G. C. et al.: Design of a novel globular protein fold with atomic-level accuracy. Science, 302, 1364-1368 (2003)[PubMed]
- Isogai, Y., Ito, Y., Ikeya, T. et al.: Design of λ Cro fold: solution structure of a monomeric variant of the de novo protein. J. Mol. Biol., 354, 801-814 (2005)[PubMed]
- Hecht, M. H., Richardson, J. S., Richardson, D. C. et al.: De novo design, expression, and characterization of Felix: a four-helix bundle protein of native-like sequence. Science, 249, 884-891 (1990)[PubMed]
- Jin, W., Kambara, O., Sasakawa, H. et al.: De novo design of foldable proteins with smooth folding funnel: automated negative design and experimental verification. Structure, 11, 581-590 (2003)[PubMed]
- Go, N.: Theoretical studies of protein folding. Annu. Rev. Biophys. Bioeng. 12, 183-210 (1983)[PubMed]
- Chikenji, G., Fujitsuka, Y. & Takada, S.: Shaping up the protein folding funnel by local interaction: lesson from a structure prediction study. Proc. Natl. Acad. Sci. USA, 103, 3141-3146 (2006)[PubMed]
- Rohl, C. A., Strauss, C. E., Misura, K. M. et al.: Protein structure prediction using Rosetta. Methods Enzymol., 383, 66-93 (2004)[PubMed]
- Fleming, P. J., Gong, H. & Rose, G. D.: Secondary structure determines protein topology. Protein Sci., 15, 1829-1834 (2006)[PubMed]
- Samish, I., MacDermaid, C. M., Perez-Aguilar, J. M. et al.: Theoretical and computational protein design. Annu. Rev. Phys. Chem., 62, 129-149 (2011)[PubMed]
著者プロフィール
略歴:2006年 神戸大学大学院自然科学研究科にて博士号(理学)取得,同年 神戸大学理学部 特別研究員,2007年 京都大学大学院理学研究科 特別研究員を経て,2007年より米国Washington大学 特別研究員.
研究テーマ:タンパク質の立体構造および機能の新規デザイン.
古賀 (巽) 理恵(Rie Tatsumi-Koga)
米国Washington大学 特別研究員.
© 2012 古賀信康・古賀 (巽) 理恵 Licensed under CC 表示 2.1 日本