細菌の細胞の大きさの制御における長期的な振動現象
田内 悠
(米国Duke大学Department of Biomedical Engineering)
email:田内 悠
DOI: 10.7875/first.author.2015.088
A noisy linear map underlies oscillations in cell size and gene expression in bacteria.
Yu Tanouchi, Anand Pai, Heungwon Park, Shuqiang Huang, Rumen Stamatov, Nicolas E. Buchler, Lingchong You
Nature, 523, 357-360 (2015)
細菌の増殖は細胞の伸長と分裂のくり返しである.この過程の連続により細胞の大きさが長期にわたりどのような挙動を示すのかについては不明なところが多いが,これは細胞の大きさの恒常性の維持の理解につながる重要な問題である.この研究においては,マイクロ流体デバイスを用いて増殖している大腸菌の細胞の大きさの時間変化を長期間にわたり観察し,その挙動を解析した.その結果,一部の個体において細胞の初期の大きさに数世代から十数世代という周期の振動が観察された.また,細胞の初期の大きさと分裂の直前の大きさとの関係はゆらぎ線形写像により表わされることがわかった.数理モデルを用いた解析により,このゆらぎ線形写像は細胞の初期の大きさの振動をひき起こすことが示された.さらに,細胞の初期の大きさだけでなく,遺伝子の発現も同様に振動することが明らかにされた.
自然界において細菌の細胞の大きさは驚くほど多様である.たとえば,海洋性バクテリオプランクトンであるSAR11群の大きさは約0.2μmであるのに対し1),Epulopiscium fishelsoniの大きさは約700μmと2),103倍もの差がある.また,同じ種であったとしても細胞の大きさは生育環境など外的な要因により大きく変動する3).細菌の細胞の大きさがどのように制御されているのかは生物学における重要な問題のひとつである.近年,分子生物学や遺伝学の発展により,細胞の大きさの制御にかかわる遺伝子やタンパク質についてしだいに明らかにされているなか,伸長と分裂のくり返しのなかで細胞の大きさがどのような時間変化を示すかというダイナミクスについてはほとんど解明されていない.従来の実験手法では,細胞の大きさを1細胞のレベルで長期間にわたり観察することが困難であったことがそのおもな理由である.
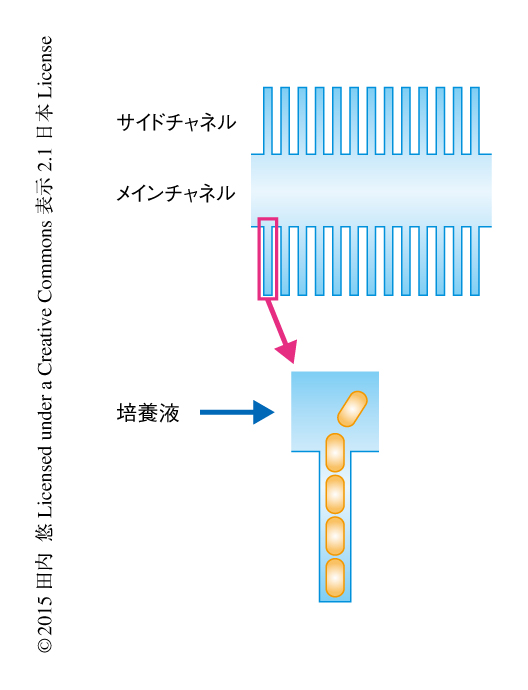
この研究においては,mother machineというマイクロ流体デバイスを用い4),大腸菌における細胞の大きさの長期的なダイナミクスを1細胞のレベルで解析することを目的にした.mother machineは中央をとおるメインチャネルとそれと垂直につながる多くのサイドチャネルから構成される(図1).サイドチャネルの幅は1つの細胞がちょうどおさまる程度で,ここに細菌をとらえその生育を観察する.サイドチャネルの幅は1細胞分しかなく片側の端は閉じているため,サイドチャネルのもっとも閉口側にある母細胞の分裂を観察しつづけることのできるのが特徴である.細菌の生育が一軸の方向に限定されるため,のちの画像解析が比較的容易であることも利点である.また,メインチャンネルにつねに培養液を流すことにより細胞の生育を定常状態に保つことができる.このデバイスを用いて,大腸菌の生育を3つの温度条件において70世代にわたり顕微鏡により観察し,画像解析したのち,データを解析した.
細胞の大きさの長期的なパターンを解析するため,個々の母細胞の系統において細胞の初期の大きさ(分裂の直後の大きさ)の自己相関関数を計算した.すると,集団平均では自己相関関数は急速に減衰し,3世代もすると相関はなくなり,とくに長期的なパターンはみられなかった.しかし,1細胞のレベルでの系統の自己相関関数をみると,約30%の細胞において初期の大きさの振動を示唆するパターンが認められた.さらに,その振動の周期は系統のあいだで必ずしも同じではなく,ある系統では8世代の周期,また,ほかの系統では16世代の周期といった現象が観察された.
どのようにして細胞の初期の大きさの振動が起こるのだろうか? そして,なぜ一部の系統でしかそれが起こらないのだろうか? 細胞周期にかかわるさまざまな物理的なパラメーターを解析したところ,初期の大きさと分裂のまえの大きさとの関係は非常にシンプルな式により記述できることがわかった.すなわち,分裂のまえの大きさyは,初期の大きさxを用いて,y = ax + b +ηという線形の関係にゆらぎηをくわえた式で記述され,これを“ゆらぎ線形写像”とよぶことにした.さらに,細胞分裂により分裂ののちの細胞の大きさが平均して半分になることをあわせると,初期の大きさx(n) の挙動は,
x(n + 1) = (ax(n) + b +η) / 2と表わされた.ここで,細胞の初期の大きさが安定するためには力学的に0 < a < 2となる必要がある.実際に,37℃における実験から得られた値はa = 0.87だった.一般的に,振動現象には負のフィードバック制御が必要である.じつは,0 < a < 2という条件それ自体が細胞の初期の大きさへの負のフィードバック制御を示している.つまり,細胞の初期の大きさが平均より小さい場合,細胞は2倍以上の大きさになってから分裂する.逆もまたしかりで,初期の大きさが平均より大きい場合,細胞は2倍以下の大きさで分裂が起こる.初期の大きさと分裂のまえの大きさとの負のフィードバックの関係性が細胞の大きさの恒常性に寄与していることが見い出された.
ゆらぎ線形写像モデルにより細胞の初期の大きさの振動現象は説明されるのだろうか? ゆらぎ線形写像の式は,一般的に1次の自己回帰モデルとして知られていたが,実験において観察されたような振動現象をひき起こすかどうかは知られていなかった.そこで,細胞の初期の大きさの挙動についてゆらぎ線形写像モデルを用いてシミュレーションにより解析した.すると,シンプルな線形式にもかかわらず,ゆらぎの存在により振動現象を起こすことが示された.しかも,この振動現象は一過性かつ確率的に起こるため,たとえば,100回のシミュレーションを行うとそのうちの一部にのみ振動が観察された.さらに,観察された振動の周期は一定ではなかった.まさに,実験において観察された細胞の初期の大きさの振動と同様の現象がシミュレーションにより再現された.つまり,ゆらぎ線形写像モデルにより細胞の初期の大きさの振動が説明されたのである.くわえて,ゆらぎ線形写像のパラメーターaが振動する確率および平均周期を決定することがシミュレーションにより示された.実際に,実験において3つの生育条件から得られたaの値はそれぞれ異なっており,それに応じて振動現象の特性が変わることが確認された.
細胞の大きさのゆらぎ線形写像モデルが遺伝子の発現にどのような影響をあたえるかについて検証した.実験に用いた大腸菌はマーカーとして蛍光タンパク質YFPを構成的に発現している.YFPの濃度のダイナミクスをゆらぎ線形写像モデルとともにシミュレーションにより解析したところ,構成的な発現にもかかわらず,YFPの濃度も細胞周期よりはるかに長い周期で振動することが示唆された.そして,この振動も細胞の初期の大きさと同様に確率的な挙動を示した.この予測をふまえて実験の結果を解析したところ,シミュレーションの結果と同様の振動が観察された.振動の周期は長いものでは10時間(約20世代)にも及び,これは,これまで大腸菌において観察された遺伝子の発現の振動のなかでももっとも長い周期のひとつであった.
筆者らの実験のデータにくわえて,先行研究から得られたデータを用いて4,5),ゆらぎ線形写像が普遍的な事象であるかどうか検証した.これらのデータは,大腸菌株,培地,使用したマイクロ流体デバイスなどの条件が異なっており,また,枯草菌を用いた研究も含んでいた.これら合計で9つの条件のデータを解析したところ,すべての条件においてゆらぎ線形写像が確認された.さらに,小規模ではあるが分裂酵母を用いて検証したところ,同様にゆらぎ線形写像が観察された.また,それぞれの条件においてゆらぎ線形写像のパラメーターaの値が異なり,小さいものでは約0.6(分裂酵母),大きいものでは約1.4(枯草菌)であった.大腸菌においてもその範囲は0.7~1.2と広がりがあった.直近の先行研究により,細菌の細胞周期における大きさの変化(分裂のまえの大きさと初期の大きさとの差)は初期の大きさにかかわらず一定であるとする“アダーモデル”が提唱されていた6-8).これは,すなわちa = 1であることを意味するが,実験条件によってはアダーモデルが必ずしも適用できるわけではないことが示唆された.
この研究により,大腸菌の細胞の大きさには長期的な振動現象がみられることがあり,それがゆらぎ線形写像という細胞の大きさの制御のモデルにより説明が可能なことが示された.また,構成的な遺伝子の発現においても長期的な振動の起こることがわかった.ゆらぎ線形写像はさまざまな条件において観察されたことから,少なくとも,細菌においては普遍的な法則であることが強く示唆された.また,遺伝子の発現の振動はストレス応答などのシグナル伝達における重要性が示されているが9),ゆらぎ線形写像による遺伝子の発現の振動は転写制御など直接的な制御機構を必要としないため,これがストレス応答などの機能をつかさどる原始的な機構である可能性も考えうる.さらに,かりに代謝系の遺伝子の発現が振動した場合,生育にどのような影響が現われるのか,そして,それがどのように遺伝子の発現にフィードバックされるのかといったことも興味深い問題である.細胞の大きさ,生育の速度,遺伝子の発現,この3つの要素のあいだにどのような相互作用があるのか.そこには基本法則が存在するのか.近年,この方面の研究が活発に進んでおり,今後,どのようなことが明らかにされるのか非常に楽しみである.
略歴:2013年 米国Duke大学大学院博士課程 修了,同年より米国Stanford大学 博士研究員.
© 2015 田内 悠 Licensed under CC 表示 2.1 日本
(米国Duke大学Department of Biomedical Engineering)
email:田内 悠
DOI: 10.7875/first.author.2015.088
A noisy linear map underlies oscillations in cell size and gene expression in bacteria.
Yu Tanouchi, Anand Pai, Heungwon Park, Shuqiang Huang, Rumen Stamatov, Nicolas E. Buchler, Lingchong You
Nature, 523, 357-360 (2015)
要 約
細菌の増殖は細胞の伸長と分裂のくり返しである.この過程の連続により細胞の大きさが長期にわたりどのような挙動を示すのかについては不明なところが多いが,これは細胞の大きさの恒常性の維持の理解につながる重要な問題である.この研究においては,マイクロ流体デバイスを用いて増殖している大腸菌の細胞の大きさの時間変化を長期間にわたり観察し,その挙動を解析した.その結果,一部の個体において細胞の初期の大きさに数世代から十数世代という周期の振動が観察された.また,細胞の初期の大きさと分裂の直前の大きさとの関係はゆらぎ線形写像により表わされることがわかった.数理モデルを用いた解析により,このゆらぎ線形写像は細胞の初期の大きさの振動をひき起こすことが示された.さらに,細胞の初期の大きさだけでなく,遺伝子の発現も同様に振動することが明らかにされた.
はじめに
自然界において細菌の細胞の大きさは驚くほど多様である.たとえば,海洋性バクテリオプランクトンであるSAR11群の大きさは約0.2μmであるのに対し1),Epulopiscium fishelsoniの大きさは約700μmと2),103倍もの差がある.また,同じ種であったとしても細胞の大きさは生育環境など外的な要因により大きく変動する3).細菌の細胞の大きさがどのように制御されているのかは生物学における重要な問題のひとつである.近年,分子生物学や遺伝学の発展により,細胞の大きさの制御にかかわる遺伝子やタンパク質についてしだいに明らかにされているなか,伸長と分裂のくり返しのなかで細胞の大きさがどのような時間変化を示すかというダイナミクスについてはほとんど解明されていない.従来の実験手法では,細胞の大きさを1細胞のレベルで長期間にわたり観察することが困難であったことがそのおもな理由である.
この研究においては,mother machineというマイクロ流体デバイスを用い4),大腸菌における細胞の大きさの長期的なダイナミクスを1細胞のレベルで解析することを目的にした.mother machineは中央をとおるメインチャネルとそれと垂直につながる多くのサイドチャネルから構成される(図1).サイドチャネルの幅は1つの細胞がちょうどおさまる程度で,ここに細菌をとらえその生育を観察する.サイドチャネルの幅は1細胞分しかなく片側の端は閉じているため,サイドチャネルのもっとも閉口側にある母細胞の分裂を観察しつづけることのできるのが特徴である.細菌の生育が一軸の方向に限定されるため,のちの画像解析が比較的容易であることも利点である.また,メインチャンネルにつねに培養液を流すことにより細胞の生育を定常状態に保つことができる.このデバイスを用いて,大腸菌の生育を3つの温度条件において70世代にわたり顕微鏡により観察し,画像解析したのち,データを解析した.
1.細胞の初期の大きさは振動する
細胞の大きさの長期的なパターンを解析するため,個々の母細胞の系統において細胞の初期の大きさ(分裂の直後の大きさ)の自己相関関数を計算した.すると,集団平均では自己相関関数は急速に減衰し,3世代もすると相関はなくなり,とくに長期的なパターンはみられなかった.しかし,1細胞のレベルでの系統の自己相関関数をみると,約30%の細胞において初期の大きさの振動を示唆するパターンが認められた.さらに,その振動の周期は系統のあいだで必ずしも同じではなく,ある系統では8世代の周期,また,ほかの系統では16世代の周期といった現象が観察された.
2.細胞の初期の大きさと分裂のまえの大きさとの関係はゆらぎ線形写像により記述される
どのようにして細胞の初期の大きさの振動が起こるのだろうか? そして,なぜ一部の系統でしかそれが起こらないのだろうか? 細胞周期にかかわるさまざまな物理的なパラメーターを解析したところ,初期の大きさと分裂のまえの大きさとの関係は非常にシンプルな式により記述できることがわかった.すなわち,分裂のまえの大きさyは,初期の大きさxを用いて,y = ax + b +ηという線形の関係にゆらぎηをくわえた式で記述され,これを“ゆらぎ線形写像”とよぶことにした.さらに,細胞分裂により分裂ののちの細胞の大きさが平均して半分になることをあわせると,初期の大きさx(n) の挙動は,
x(n + 1) = (ax(n) + b +η) / 2と表わされた.ここで,細胞の初期の大きさが安定するためには力学的に0 < a < 2となる必要がある.実際に,37℃における実験から得られた値はa = 0.87だった.一般的に,振動現象には負のフィードバック制御が必要である.じつは,0 < a < 2という条件それ自体が細胞の初期の大きさへの負のフィードバック制御を示している.つまり,細胞の初期の大きさが平均より小さい場合,細胞は2倍以上の大きさになってから分裂する.逆もまたしかりで,初期の大きさが平均より大きい場合,細胞は2倍以下の大きさで分裂が起こる.初期の大きさと分裂のまえの大きさとの負のフィードバックの関係性が細胞の大きさの恒常性に寄与していることが見い出された.
3.細胞の大きさの振動はゆらぎ線形写像モデルにより説明される
ゆらぎ線形写像モデルにより細胞の初期の大きさの振動現象は説明されるのだろうか? ゆらぎ線形写像の式は,一般的に1次の自己回帰モデルとして知られていたが,実験において観察されたような振動現象をひき起こすかどうかは知られていなかった.そこで,細胞の初期の大きさの挙動についてゆらぎ線形写像モデルを用いてシミュレーションにより解析した.すると,シンプルな線形式にもかかわらず,ゆらぎの存在により振動現象を起こすことが示された.しかも,この振動現象は一過性かつ確率的に起こるため,たとえば,100回のシミュレーションを行うとそのうちの一部にのみ振動が観察された.さらに,観察された振動の周期は一定ではなかった.まさに,実験において観察された細胞の初期の大きさの振動と同様の現象がシミュレーションにより再現された.つまり,ゆらぎ線形写像モデルにより細胞の初期の大きさの振動が説明されたのである.くわえて,ゆらぎ線形写像のパラメーターaが振動する確率および平均周期を決定することがシミュレーションにより示された.実際に,実験において3つの生育条件から得られたaの値はそれぞれ異なっており,それに応じて振動現象の特性が変わることが確認された.
4.構成的な遺伝子の発現も振動する
細胞の大きさのゆらぎ線形写像モデルが遺伝子の発現にどのような影響をあたえるかについて検証した.実験に用いた大腸菌はマーカーとして蛍光タンパク質YFPを構成的に発現している.YFPの濃度のダイナミクスをゆらぎ線形写像モデルとともにシミュレーションにより解析したところ,構成的な発現にもかかわらず,YFPの濃度も細胞周期よりはるかに長い周期で振動することが示唆された.そして,この振動も細胞の初期の大きさと同様に確率的な挙動を示した.この予測をふまえて実験の結果を解析したところ,シミュレーションの結果と同様の振動が観察された.振動の周期は長いものでは10時間(約20世代)にも及び,これは,これまで大腸菌において観察された遺伝子の発現の振動のなかでももっとも長い周期のひとつであった.
5.先行研究のデータにおけるゆらぎ線形写像モデルの検証
筆者らの実験のデータにくわえて,先行研究から得られたデータを用いて4,5),ゆらぎ線形写像が普遍的な事象であるかどうか検証した.これらのデータは,大腸菌株,培地,使用したマイクロ流体デバイスなどの条件が異なっており,また,枯草菌を用いた研究も含んでいた.これら合計で9つの条件のデータを解析したところ,すべての条件においてゆらぎ線形写像が確認された.さらに,小規模ではあるが分裂酵母を用いて検証したところ,同様にゆらぎ線形写像が観察された.また,それぞれの条件においてゆらぎ線形写像のパラメーターaの値が異なり,小さいものでは約0.6(分裂酵母),大きいものでは約1.4(枯草菌)であった.大腸菌においてもその範囲は0.7~1.2と広がりがあった.直近の先行研究により,細菌の細胞周期における大きさの変化(分裂のまえの大きさと初期の大きさとの差)は初期の大きさにかかわらず一定であるとする“アダーモデル”が提唱されていた6-8).これは,すなわちa = 1であることを意味するが,実験条件によってはアダーモデルが必ずしも適用できるわけではないことが示唆された.
おわりに
この研究により,大腸菌の細胞の大きさには長期的な振動現象がみられることがあり,それがゆらぎ線形写像という細胞の大きさの制御のモデルにより説明が可能なことが示された.また,構成的な遺伝子の発現においても長期的な振動の起こることがわかった.ゆらぎ線形写像はさまざまな条件において観察されたことから,少なくとも,細菌においては普遍的な法則であることが強く示唆された.また,遺伝子の発現の振動はストレス応答などのシグナル伝達における重要性が示されているが9),ゆらぎ線形写像による遺伝子の発現の振動は転写制御など直接的な制御機構を必要としないため,これがストレス応答などの機能をつかさどる原始的な機構である可能性も考えうる.さらに,かりに代謝系の遺伝子の発現が振動した場合,生育にどのような影響が現われるのか,そして,それがどのように遺伝子の発現にフィードバックされるのかといったことも興味深い問題である.細胞の大きさ,生育の速度,遺伝子の発現,この3つの要素のあいだにどのような相互作用があるのか.そこには基本法則が存在するのか.近年,この方面の研究が活発に進んでおり,今後,どのようなことが明らかにされるのか非常に楽しみである.
文 献
- Rappe, M. S., Connon, S. A., Vergin, K. L. et al.: Cultivation of the ubiquitous SAR11 marine bacterioplankton clade. Nature, 418, 630-633 (2002)[PubMed]
- Angert, E. R., Clements, K. D. & Pace, N. R.: The largest bacterium. Nature, 362, 239-241 (1993)[PubMed]
- Chien, A. -C., Hill, N. S. & Levin, P. A.: Cell size control in bacteria. Curr. Biol., 22, R340-R349 (2012)[PubMed]
- Wang, P., Robert, L., Pelletier, J. et al.: Robust growth of Escherichia coli. Curr. Biol., 20, 1099-1103 (2010)[PubMed]
- Moffitt, J. R., Lee, J. B. & Cluzel, P.: The single-cell chemostat: an agarose-based, microfluidic device for high-throughput, single-cell studies of bacteria and bacterial communities. Lab Chip, 12, 1487-1494 (2012)[PubMed]
- Amir, A.: Cell size regulation in bacteria. Phys. Rev. Lett., 112, 208102 (2014)
- Taheri-Araghi, S. Bradde, S., Sauls, J. T. et al.: Cell-size control and homeostasis in bacteria. Curr. Biol., 25, 385-391 (2015)[PubMed]
- Campos, M., Surovtsev, I. V., Kato, S. et al.: A constant size extension drives bacterial cell size homeostasis. Cell, 159, 1433-1446 (2014)[PubMed]
- Levine, J. H., Lin, Y. & Elowitz, M. B.: Functional roles of pulsing in genetic circuits. Science, 342, 1193-1200 (2013)[PubMed]
著者プロフィール
略歴:2013年 米国Duke大学大学院博士課程 修了,同年より米国Stanford大学 博士研究員.
© 2015 田内 悠 Licensed under CC 表示 2.1 日本